Set expressions
1 Set Expressions
\[ \{ x \, |\, f(x) \} \\ \{ x \in \mathbb { R } \, |\, \sqrt { x-2 } \} \quad \quad \{ x \in \mathbb { R } \, |\, x ^{ 2 } = -1\} \\ x+2y=7 \Rightarrow \{ (x,y) \, |\, x+2y=7 \} \\ \{ x \, |\, x \in \mathbb { N }, 5>x>1 \} \Rightarrow \{ 2,3,4 \} \\ \{ 2,3,4 \} \Rightarrow [2,4] \\ \]
2 Operators and set calculations
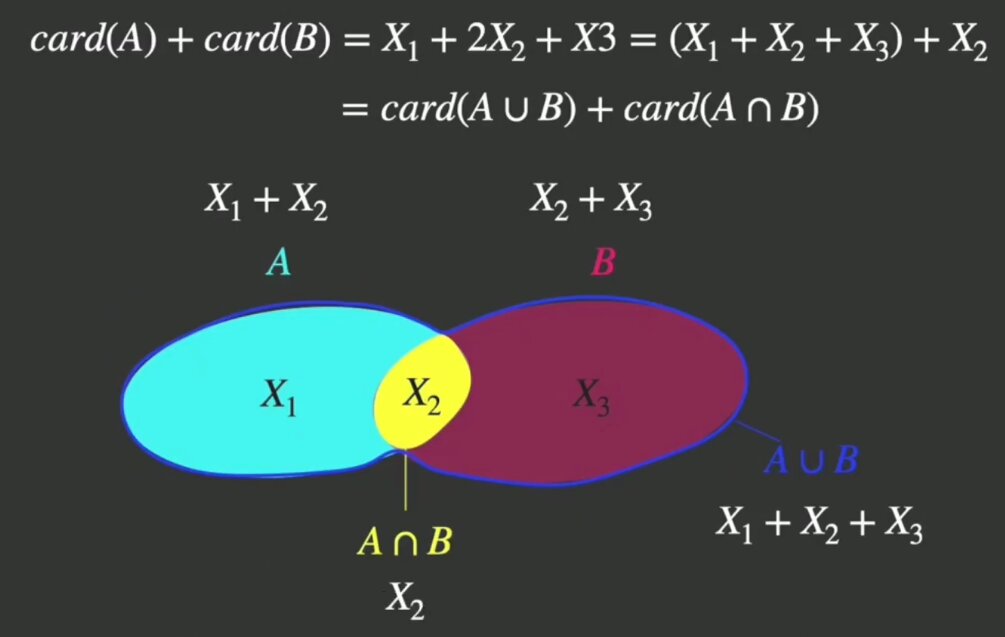
\[ \{ 1,2,3,4,5 \} \cup \{ 3,4,5,6,8 \} = \{ 3,4,5 \} \\ \{ (x,y) \, |\, y=0 \} \cap \{ (x,y) \, |\, x=0 \} = \{ (0,0) \} \\ \]

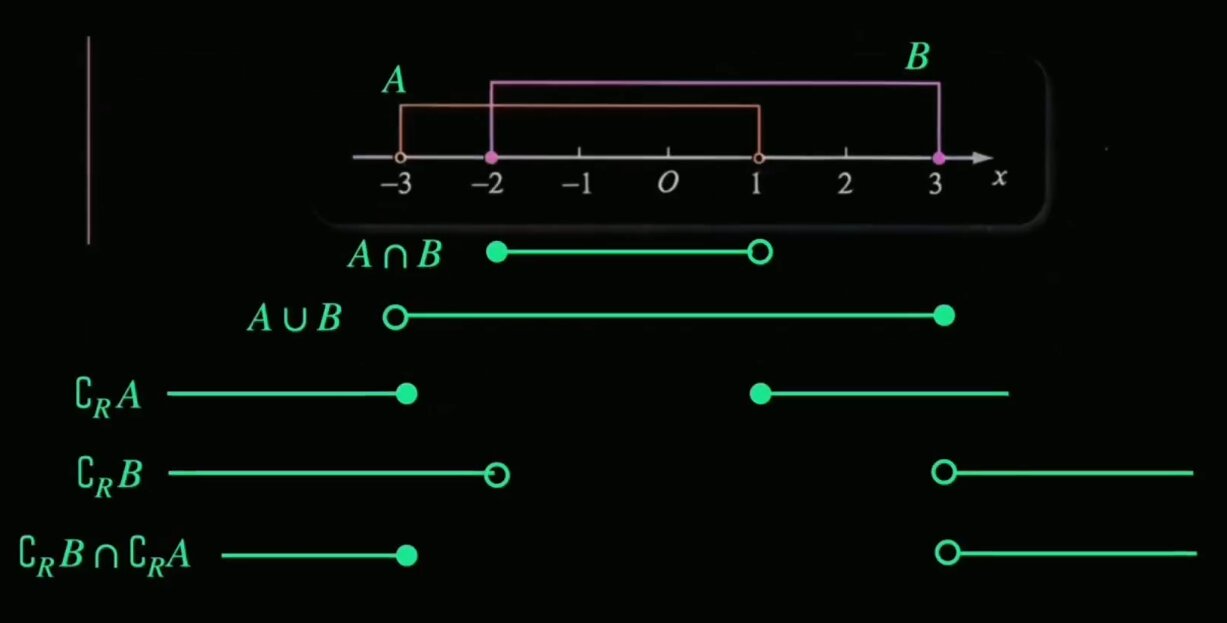
\[ 1) A \cup \complement _u B \quad \quad 2) (A \cap \complement _u B) \cup (B \cap \complement _u A) \\ \]
3 Definition of a graph
First quarter:
\[ \{ (x,y) \, |\, x>0 \} \cup \{ (x,y) \, |\, y>0 \} \\ = \{ (x,y) \, |\, x>0, y>0 \} \\ \]
A dot:
\[ \{ (x,y) | \, |\, x=1, y=3 \} \\ \{ (x,y) \, |\, y=0 \} \cap \{ (x,y) \, |\, x=0 \} \\= \{ (x,y) \, |\, y=0, x=0 \} \\ \]
A line:
\[ \{ (x,y) \, |\, y=2x+3 \} \\ \Rightarrow \{ (x,y) \, |\, (x_1,y_1), (x_2,y_2),(x_3,y_3)\, ... \} \]